CRITERIO DE LA SEGUNDA DERIVADA
El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
Teorema
Sea  una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
Si  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
Si 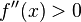 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
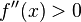 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Si  , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
Uno de los ordenes de derivación es el de la segunda derivada, aunque no es despreciable la utilización de las derivadas de orden superior, sobre todo en cálculo de errores. Curiosamente las aplicaciones físicas implican, por lo general, derivadas de segundo orden como podría ser las ecuaciones de movimiento.
En esta sección presentaremos una interpretación gráfica de los criterios de la segunda derivada que nos servirá para poder obtener los máximos o mínimos de una función. Antes de analizar como es la relación de la segunda derivada conoceremos algunas definiciones:
Definición.
Cóncava hacia abajo. Se dice que una función es cóncava hacia abajo cuando la primera derivada es creciente en un intervalo abierto (a,b)



Definición.
Puntos de inflexión y número de inflexión. Sea f una función y a un número. Supongamos que existe números b y c tales que b<a<c y además:
a) f es una función continua en el intervalo abierto (b,c)
b) f es una función cóncava hacia arriba y cóncava hacia abajo en (a,c), o viceversa.
Bajo las condiciones anteriores el punto (a,f(a)) se llama punto de inflexión, y al número a se llama número de inflexión.
Si la segunda derivada f´´ de una función f es positiva en un intervalo abierto (a,b) es porque la primera derivada f´ es creciente en ese intervalo.



Criterios de la segunda derivada para máximos y mínimos relativos
Sea f una función con su primera derivada definida, al menos, en un intervalo abierto conteniendo al número a. Si f´´ esta definida entonces podemos considerar los siguiente aspectos:
a).- Si f´(a)=0 y f´´(a)<0 entonces se dice que f tiene un máximo local en a.
b).- Si f´(a)=0 y f´(a)>0 entonces se dice que f tiene un mínimo local en a.
webgrafía:
http://es.wikipedia.org/wiki/Criterio_de_la_segunda_derivada
http://dieumsnh.qfb.umich.mx/DIFERENCIAL/criterio_de_la_segunda_derivada.htm
http://profecarlinis.galeon.com/album1608406.html
No hay comentarios:
Publicar un comentario