APLICACIÓN DE LAS INTEGRALES EN LA ARQUITECTURA
La aplicación de las integrales en la arquitectura es muy variada, su principal objetivo es crear diseños en edificaciones con formas complejas y dinámicas.
Las integrales forman parte de los cálculos ha realizarse con precisión para determinar resultados óptimos en el proyecto


ESTADIO ALLIANZ ARENA
Para realizar estos cálculos y crear edificaciones con curvaturas y formas el arquitecto mismo debe conocer una multiplicidad de principios que componen el proceso de diseño, su materialización y estructuración física que se concluyen en la obra construida. El diseño debería entenderse como un aspecto integral y no como un objeto que se compone a partir de diversos sistemas

MUSEO DE ARTE CONTEMPORÁNEO DE NITEROI

MUSEO OSCAR NIEMEYER

MUSEO DE ARTE MODERNO
MUSEO POMPIDOU
La aplicación de las integrales también se centra en edificios que tienen una figura amorfa, donde el cálculo de su área resulta complejo.

EDIFICIO INFOSYS

MUSEO DE DENVER
Algunas fórmulas que permiten calcular áreas y volúmenes son:
Cálculo de áreas planas:
A= 

Cálculo de volúmenes:

webgrafía:
- http://es.slideshare.net/franklingualaquiza/aplicacin-de-la-integral-definida-en-la-arquitectura
- http://www.inetor.com/indefinidas/formulas_integrales.html
- http://bjglez.webs.ull.es/aplicaciones_de_la_integral.pdf


 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  y la segunda derivada de
y la segunda derivada de 
 , entonces
, entonces  .
.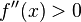 , entonces
, entonces  , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es, 



 .
. '
' cambia de positiva a negativa en
cambia de positiva a negativa en  .
. no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.


 que contiene a
que contiene a